Effective Nuclear Charge

The allowed values of energy for an electron in hydrogen atom are given by the expression.

Accordingly for hydrogen atom (Z =1, n = 1), E = -R and the energy of the outermost electron calculated form equation agrees with the observed ionization energy 1312KJ mol^-1 . This agreement is not observed for atoms other than hydrogen, that is , for atoms with Z > 1. For example. He (Z =1, n =1), the calculated E (E_calc) according to equation is 5248 kJ mol^-1, whereas he first ionization potential(E_obsis 2372kJ mol^-1   only. For Li (  z = 3, n =2), the ( (E_calc 2952  KJ mol^-1 but E_obs ( 1st  ionizationptenital  = 520 KJ mol^-1. This disagreement holds good for all other elements. The observed ionization energy, of say Li, is considerable lower than that calculated form equation , for reasons :

(i)    The expression does not hold good for multi-electron atoms because it does not take inter-electronic repulsions into account.
(ii)    The 2s¹ electron does not face the nuclear change directly. There is an intervening core of 1s2 electrons which not only shield the nucleus but also repels the 2s¹ electron, thereby facilitating its easier removal.

In other words, the inner core of electrons shields or screen he nucleus for outer electrons. Consequently, the outer electrons experience only a part of the nuclear change. In other words, the effective nuclear charge faced by the outer electrons is lower than that expected form total nuclear change. In case of Li, the effective nuclear change faced by 2s¹ electron is not 3 but between 1 and 2 (actual). However, if we recall the radial probability distribution curve of 2_s orbital in hydrogen like atom, It is apparent that 2_s electron has definite probability of finding itself near the nucleus and hence would penetrate the inner 1_s orbital core. This means that although 2s electron is shielded by the 1s core yet the 2_s electron penetrates it to some extent and experiences somewhat higher nuclear charge. This is also illustrated in where 3s¹ electron in Na atom penetrates the inner core of Na+ and experiences a higher nuclear charge. It may also be understood that this does not mean the energy of 2s electron in Li varies as it penetrates the 1s orbital. In fact the energy of outer electron is determined by the effective nuclear change which is less than Z (nuclear charge) by an amount contributed as shielding constant (s) of the intervening core of electrons.
                                      
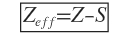
If we recall radial probability distribution curves, say for n = 3, we find that although the most “probable radius” decreases in the order 3s > 3p >3d , yet the positions and presence of three reigns of high probability in 3s electron penetrates more into a region close to the nucleus than 3p and the order of penetration for a given n is
                                               S > P > d > f
                                      
Due to grater penetration, s-electrons will tend to shield the nucleus more effectively than p-electrons which, in true, will shield the nucleus more festively than d-electron. That is for a given n, the screening or shielding varies as
                                                S > P > d > f

For more help in Effective Nuclear Charge click the button below to submit your homework assignment