Laplacian Operator
Laplacian Operator Assignment Help | Laplacian Operator Homework Help
Laplacian Operator
This is a very common operator used in quantum mechanics. It is represented by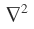 (pronounced as ‘del squared’) and is defined as
(pronounced as ‘del squared’) and is defined as
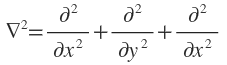
This Schrodinger wave equation viz.,
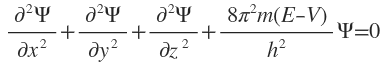
May be written in terms of Laplacian operator as
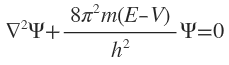
Hamiltonian operator. Schrodinger wave equation as written above may be rewritten in the form
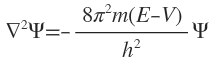
or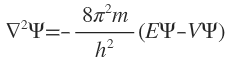
or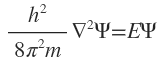
or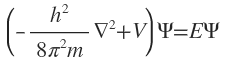
This equation implies that the operation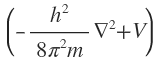 carried on the function
carried on the function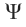 , is equal to the total energy multiplied with the function
, is equal to the total energy multiplied with the function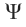 .
.
The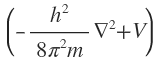 operator is called Hamiltonian operator and is represented by
operator is called Hamiltonian operator and is represented by 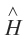 . Thus
. Thus
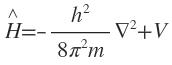
Eqn may, therefore, be written as
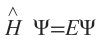
This is another short-hand form of writing the Schrödinger wave equation.
As mentioned earlier,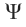 is called the eigen function and E called eigen value.
is called the eigen function and E called eigen value.
Such an equation is, therefore, called eigen value equation. Thus for Schrödinger wave equation, we can write
(Energy operator)(Wave function) = (Energy)X(Wave function)
This result can be generalized as it is equally applicable to all other observables i.e. measurable properties of a system. Thus, in general, we can write
(Operator corresponding to an observable) (Wave function)
= (Value of observable)X( Wave function)
Thus if we know both the wave function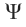 and the operator for the observable and if the wave function is an eigen function, we can predict the mechanics given in the next section.
and the operator for the observable and if the wave function is an eigen function, we can predict the mechanics given in the next section.
For more help in Laplacian Operator click the button below to submit your homework assignment
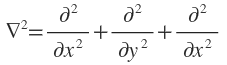
This Schrodinger wave equation viz.,
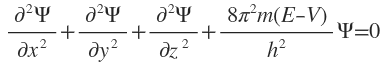
May be written in terms of Laplacian operator as
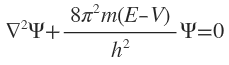
Hamiltonian operator. Schrodinger wave equation as written above may be rewritten in the form
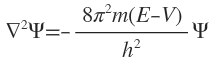
or
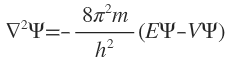
or
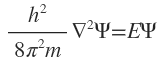
or
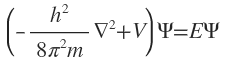
This equation implies that the operation
The
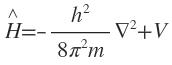
Eqn may, therefore, be written as
This is another short-hand form of writing the Schrödinger wave equation.
As mentioned earlier,
Such an equation is, therefore, called eigen value equation. Thus for Schrödinger wave equation, we can write
(Energy operator)(Wave function) = (Energy)X(Wave function)
This result can be generalized as it is equally applicable to all other observables i.e. measurable properties of a system. Thus, in general, we can write
(Operator corresponding to an observable) (Wave function)
= (Value of observable)X( Wave function)
Thus if we know both the wave function
For more help in Laplacian Operator click the button below to submit your homework assignment