Cyclomatic Complexity
Cyclomatic Complexity Assignment Help | Cyclomatic Complexity Homework Help
Cyclomatic Complexity
The cyclomatic complexity is also known as structural complexity because if gives internal view of the code. This is used to find the number of independent paths through a program. This provides the upper bound for the number of tests that must be conducted to ensure that all statements have been executed at least once and every condition has been executed on its true and false side. If a possible to define a set of branch then it may have infinite number of paths. It is possible to define a set of algebraic expressions that gives the total number of possible paths through a program however, using total number of paths that has been found to be impractical. Because of this complexity erasure is defined in terms of independent paths. An independent path is any though the program that introduces at least are new set of processing statements or new conditions.
McCabe’s cyclomatic metric V(G) of a graph G with n vertices, e edges and p connected component is V(G) = e – n + 2P.
Given a program we will associate with it a directed graph that has unique entry and exit nodes. Each node in the graph corresponds to a block of code in the program where the flow is essential and the arcs correspond to branches taken in the program. This graph is known as flow graph and it is assumed that each node can be reached by the entry node and each node can reach the exist node.
For example and flow graph is shown below with entry ‘I’ and exit node ‘6’.
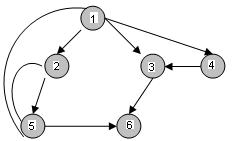
The value of cyclomatic complexity can be calculated as
V(G) = 9 – 6 + 2 = 5
where e = 9, n = 6 and p = 1
There will be five independent paths for the flow graph illustrated.
PATH 1 : 1 3 6
PATH 2 : 1 2 5 6
PATH 3 : 1 4 3 6
PATH 4 : 1 2 5 1 3 6 or 1 2 5 1 2 5 6
PATH 5: 1 2 5 2 5 6
Properties of cyclomatic complexity are :
1. V(G) > 1
2. V(G) is the maximum number of independent path in graph G.
3. Inserting and deleting functional statements to G does not effect V(G).
4. G has only one path if and only if V(G) = 1.
5. Inserting a new row in G increases V(G) by unity.
6. V(G) depends only on the decision structure of G.
For more help in Cyclomatic Complexity click the button below to submit your homework assignment
McCabe’s cyclomatic metric V(G) of a graph G with n vertices, e edges and p connected component is V(G) = e – n + 2P.
Given a program we will associate with it a directed graph that has unique entry and exit nodes. Each node in the graph corresponds to a block of code in the program where the flow is essential and the arcs correspond to branches taken in the program. This graph is known as flow graph and it is assumed that each node can be reached by the entry node and each node can reach the exist node.
For example and flow graph is shown below with entry ‘I’ and exit node ‘6’.
The value of cyclomatic complexity can be calculated as
V(G) = 9 – 6 + 2 = 5
where e = 9, n = 6 and p = 1
There will be five independent paths for the flow graph illustrated.
PATH 1 : 1 3 6
PATH 2 : 1 2 5 6
PATH 3 : 1 4 3 6
PATH 4 : 1 2 5 1 3 6 or 1 2 5 1 2 5 6
PATH 5: 1 2 5 2 5 6
Properties of cyclomatic complexity are :
1. V(G) > 1
2. V(G) is the maximum number of independent path in graph G.
3. Inserting and deleting functional statements to G does not effect V(G).
4. G has only one path if and only if V(G) = 1.
5. Inserting a new row in G increases V(G) by unity.
6. V(G) depends only on the decision structure of G.
For more help in Cyclomatic Complexity click the button below to submit your homework assignment