The Marginal Rate of Substitution

Look at one of the indifference curves in Figure 3.4. The slope of the curves is of central importance. Think about what the slope means: If you choose some basket on one of the curves, how much would you be willing to give up of good 2 to get one more unit of good 1? If you would be willing to give up only a small quantity of good 2, the magnitude of the slope would be small, whereas if you were willing to give up a lot, it would be large.

Imagine that we have two individuals who each have 5 apples (good 1) and 5 bananas (good 2). To get one more apple, the first is willing to give up one banana, whereas the other is willing to give up two bananas. The first individual’s indifference curve running through the point (5,5) will then slope less than the second individual’s indifference curve. These two individuals have different tastes regarding apples and bananas.

The numerical value of the slope of an indifference curve, the magnitude of the slope, is called the marginal rate of substitution (MRS), and it can approximately be calculated as



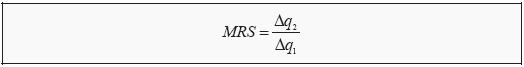
Here, delta q1 and delta q2 are the changes in quantity for good 1 and good 2, respectively. Individual 2 above was willing to give up 2 bananas to get one more apple. Then delta q2 = -2, delta q1 = 1, and marginal rate of substitution (MRS) = -2/1 = -2. The fact that the indifference curves slope less and less to the right implies that marginal rate of substitution (MRS) is decreasing. Often, one does not keep the minus sign in MRS. It is then implicitly understood that one gets less (minus) of one good to get more (plus) of the other. Note that, if one leaves out the minus in marginal rate of substitution (MRS), one typically does so for marginal rate of transformation (MRT) as well.

The expression for marginal rate of substitution (MRS) above is only approximate. The smaller one chooses Δq1, the better the approximation will be. For it to become completely exact, Δq1 must be chosen infinitely small. This, in turn, makes it necessary to use derivatives. That, however, lies outside the scope of this book. Note that the word "marginal" means "infinitely small.” You will hear that word many times in economics.