Charge and Discharge of a Capacitor through a Resistor

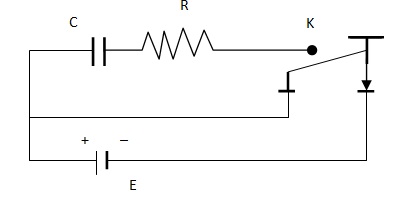
(a)    Growth of Charge.  A capacitor C and a resistance R are connected to a cell of emf E through a Morse Key K. When the key is pressed, a momentary current I flow through R. At any instant t, let Q be the charge on the capacitor of capacitance C.
P.D. across capacitor = Q/C
P.D. across resistor = RI
The emf equation of the circuit is
E = (Q/C) + RI ___________________________________________________________… (1)
E = (Q/C) + R (dQ/dt)
: .  I = dQ/dt/
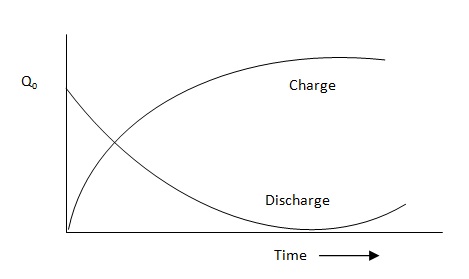
The capacitor continues getting charge till it attains the maximum charge Q0. At that instant I = dQ/dt = 0. The P.D. across the capacitor is E. = Q₀/C.
i.e., when,         Q = Q₀, dQ/dt = 0 and E = Q₀/C
. :            Q₀/C = Q/C + R dQ/dt
        (Q₀ – Q) = CR dQ/dt
        [dQ /Q₀ – Q] = dt/CR ________________________________________________  … (2)

Integrating, - loge (Q₀ – Q) = t /CR + K               
Where K is a constant.
When t = 0, Q = 0      . : - loge Q₀ = K
. :         - loge (Q₀ – Q) = t/CR – loge Q₀
        loge (Q₀ – Q) =  - t/CR + loge Q₀
    loge (Q₀ – Q) – loge Q₀ = - t/CR
        loge (Q₀ – Q/Q₀) = - t/CR
        Q₀ – Q/Q₀ = e –t/CR or 1 – Q/Q₀ = e-1/CR
            Q = Q₀ (1 - e-1/CR)                             … (3)

The term CR is called time constant of the circuit.
At the end of time t = CR, Q = Q₀ (1-e-1/CR) = 0.632Q₀
Thus, the time constant may be defined as the time taken by the capacitor to get charged to 0.632 times its maximum value.
The rate of growth of charge is dQ/dt = Q₀/CR e-1/CR = 1/CR (Q₀ – Q)
Thus it is seen that smaller the product CR, the more rapidly does the charge grow on the capacitor.
The rate of growth of the charge is rapid in the beginning and less as the charge approaches nearer and nearer by the steady values.



(b)    Decay of charge (Discharging of a Capacitor through Resistance)
Let the capacitor having charge Q0 be now discharged by releasing the Morse Key K. The charge flows out of the capacitor and this constitutes a current. In this case E = 0.
        R dQ/dt + Q/C = 0                        _____________________________________________… (1)
Or         dQ /C = -1/CRdt   
Integrating, loge Q = -t/CR + K, where K is a constant
When t = 0, Q = Q₀    . : loge Q₀ = K
            loge Q = - t/CR + loge Q₀
or            loge Q/Q₀ = - t/CR or Q/Q₀ = e-1/CR
. :            Q = Q₀ e-1/CR                       ____________________________________________  … (2)

This shows that the charge in the capacitor decays exponentially and becomes zero after infinite interval of time.
This rate of discharge is
        I – dQ/dt = - Q0/CR e – t/CR = - Q/CR                ___________________________________… (3)

Thus, smaller the time-constant CR, the quicker is the discharge of the capacitor.
In Eq. (2), if we put t = Cr, then Q = Q₀ e-1 = 0.368Q₀.
Hence time constant may also be defined as the time taken by the current to fall from maximum to 0.368 of its maximum value,