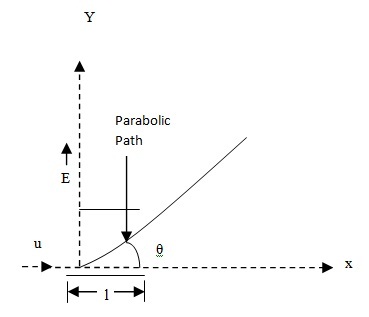
Motion of Charged Particle in Electric Field  (Transverse Electric Field)

Let the charged particle be moving with an initial uniform velocity u in the X-direction and the constant electric field be applied in the Y-direction. Then at time t = 0, we have
        v_x = u, v_y = v_z = 0 and x = y = z = 0
There is no acceleration along X and Z-direction (ax = az = 0).
            a_y = qEy/m = qE/m                            … (1)
Here, m is the mass and q is the charges of the particle.
But the particle has got an initial velocity in the X-direction. Hence, it will continue to move in the X-direction with the same velocity.
        . :     v_x = u, v_y = qE/m.t, v_z = 0                        … (2)

Integrating these equations w.r.t. time t, we get displacements along the three axes,
            x = ut, y = ½ qE/m t²     and     z = 0                    … (3)

Eliminating t between the equation of x and y.
            y = ½ qE/m . (x/u)²
Or            x² = 2mu²/qE.y = Ky                            … (4)

Where K is a constant. This equation represents a parabola.

The transverse displacement suffered by the particle during passage through the plate of length l is
    y1 = 1/2at² = ½ . qE/m . (l/u)² = qEt²/2mu²                             … (5)

When the particle leaves the field, it follows a straight ling path which is tangent to the parabola. Its direction of travel after emerging from the field is inclined to the original of travel (x-axis) by an angle θ give by
    Tan θ = vy/vx = qE/mu .t = qEl/mu²     (. : t = l/u)                    … (6)

This principle is used in cathode ray oscillographs and in television pictures tubes.



For more help in Motion of Charged Particle in Alternating Electric Field please click the button below to submit your homework assignment.