Determination of Self- Induction by Raleigh’s method

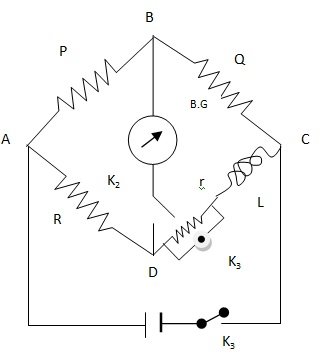
The coil, whose self-inductance L is to be connected in the fourth arm of a Wheat stone’s bridge plug key K₃ is connected across r so that it may be short-circuited. P, Q and R are non-inductive resistances.

(a)    Initially, K₃ is kept closed. The ohmic resistance S of the inductance coil alone is included in the fourth arm. P is made equal to Q. Then R is adjusted for no deflection in the B.G., by first pressing battery key K₁ and then galvanometer key K₂. Under this condition, no current flows through the galvanometer.

(b)    If now the galvanometer key2 is closed first and then the battery key K₁, then a throw θ₁ is observed in the galvanometer. This throw arises due to an extra emf L di/dt induced in the coil while the current is growing. If G is galvanometer resistance, then current through it due to induced emf is

i’ = kL /G di /dt
Where k is constant which depends upon the relative resistance in the circuit. 

Hence the total charge passing through the galvanometer, as the current in the coil grows from zero to a steady maximum value i0 is given by

    q = ∫ⁱ₀ I dt = kL /G ∫ⁱ₀  di/ dt dt =  kL /G i₀    ______________________________… (1)

If θ1 be the first throw of the galvanometer, then,
    Q = K θ₁ (1 + λ /2)  _________________________________________________ … (2)
. :     kL/G i₀ = K θ₁ [1 + λ /2]  ____________________________________  (from 1 and 2)
    = T/2π C /nBA. θ₁ [1 + λ /2]

(c)    To eliminate k and i0, the key K₃ is opened and the resistance r is included in the arm CD. As r is small, it does not affect the current i0 in the arm CD appreciably. But it will introduce an additional emf ri₀ in the arm CD: This causes a steady current (Kr/G)i₀ through the galvanometer. K₁ is closed first and then K₂. The steady deflection Φ in the galvanometer is noted. Then,
(kr /G) i₀ = C /nBA Φ.

Here, C /nAB is the current reduction factor of the galvanometer.

Dividing (3) by (4),
        L /r = T /2π θ₁ / Φ [1 + λ/2]
Or         L = rT /2π θ₁ / Φ [1 + λ/2]





For more help in Determination of Self- Induction by Raleigh’s method click the button below to submit your homework assignment