Gouy’s Method for Measurement of Susceptibility

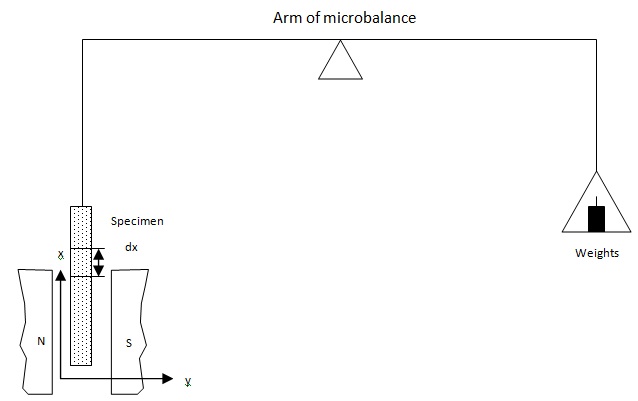
Apparatus. It consists of an electromagnet having parallel and flat pole pieces with a gap between them. The electromagnet provides a strong horizontal magnetic field of nearly 1 Wb m-2.

The sample under test is taken in the form of a thin rod. It is suspended vertically from one arm of a sensitive micro balance in the magnetic field between the wedge shaped pole pieces of the electromagnet. The specimen is suspended in such a way that its lower end is near the midpoint of the magnetic field where the magnetic intensity H is large while its upper end is outside the field in the region of low intensity H0. The cylindrical rod is then weighed by suspended it from a sensitive microbalance in the two cases:
(i)    When field is off.            (ii) when field is on.

Theory. Let μ₁ and μ₂ be the permeability of air and specimen respectively. Consider a magnetic field of intensity H in a region. Let V be the volume of the specimen. Hence the energy of magnetic flux in this region is 1/2 μ₁H₂V before inserting the specimen and 1/2 μ₂H₂V, after inserting the specimen. The difference of these energies is equal to the work done is inserting the specimen,
        . : Work done = 1/2 (μ₂ – μ₁) H₂V
This is stored as potential energy of field.
Change in potential energy of field,
        U = 1/2 (μ₂ – μ₁) H₂V                                … (1)

We have, μr = 1 + χm     or    μ/μ₀ = 1+ χm

. :    μ = μ₀ + μ₀ χm
Let χ1 and χ2 be the susceptibilities of air and specimen. Then,
    μ₁ = μ₀ + μ₀χ1 and μ₂ = μ₀ + μ₀ χ₂
. :    μ₂ – μ₁ = μ₀ (χ₂ – χ₁)                                    … (2)

Substituting this in Eq. (1), we get
    U = 1/2 μ₀ (χ₂ – χ₁) H₂V                                    … (3)

Let Fx be the force acting on the specimen along x-axis. Then,
    F = - dU/dx – d{1/2μ₀ (χ₂ – χ₁)H₂V}/dx
        = -1/2 μ₀ (χ₂ – χ₁) d(H₂)V/dx

If H_x, H_y and H_z are components H, then
    H₂ = Hx₂ + Hy₂ + Hz₂
. :    F = - 1/2 μ₀ (χ₂ – χ₁) {d(Hx₂ + Hy₂ + Hz₂)/dx}V                        … (4)

Now, considering X-axis to be vertical, the vertical force on a small element dx of rod of volume dV, at a distance x from origin is
    dF_x = - μ₀ (χ₂ – χ₁) [H_x dH_x/d_x + H_y dH_y/d_x + H_z dH_z/d_x] dV

Let α be cross-sectional area of rod. Then,
    d_v = α d_x
. :    dF_x = - μ₀(χ₂ – χ₁)[H_x dH_x/d_x + H_y dH_y/x + H_z dH_z/d_x]adx                    … (5)

In the narrow gap between pole pieces, the magnetic flux will consists of straight lines direct from one pole face to another, in y direction say. Thus only the component Hy will be of significant magnitude while Hx and Hz will be negligible. Hence Eq. (5) is expressible as
    dF_x = - μ₀ (χ₂ – χ₁) H_y dH_y/dz adx                                … (6)

The total vertical force on the rod due to whole field variation along the length under the limit H_y = H to H_y = H₀ is
    Fx = - μ₀ (χ₂ – χ₁) a ∫H₀ H_y dH_y dx/dx
        = - μ₀ (χ₂ – χ₁) a ∫H₀ Hy dH_y
        = - μ₀ (χ₂ – χ₁) a [H_y²/2]H^Ho
        = - 1/2μ₀ (χ₂ – χ₁) a (H₀₂ – H₂)                             … (7)

Let m₁ and m₂ be the weights to counterpoise the force on rod with magnetic field off and on respectively. Then,   
        F_x = (m₂ – m₁)g.                                    … (8)
Equation (7) and (8), we get
        (m₂ –m₁)g = 1/2μ₀ (χ₂ – χ₁) a (H₂ – H₀²)
    (χ₂ – χ₁) = 2(m₂ – m₁)g / μ₀ a(H₂ – H₀²)                            … (9)

H₀ and H can be measured by the flux meter. Thus by putting the susceptibility of air χ₁ and other known quantities in the above equations, χ₂ is calculated.