Grassot Flux meter

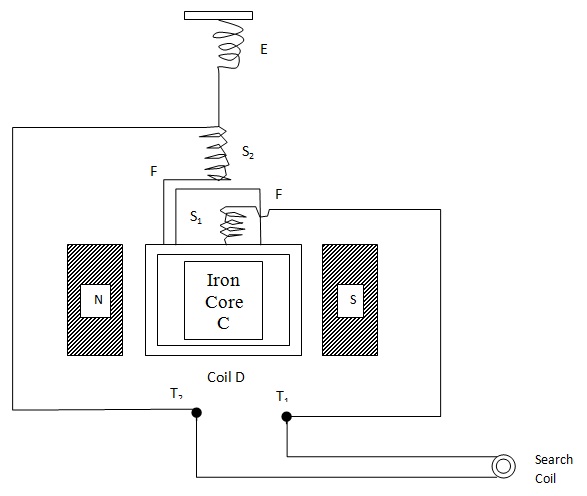
It is used for measuring magnetic flux. It is a special type of ballistic galvanometer. In it the restoring torque is made negligibly small and the electromagnetic damping large.

Construction. It consists of a coil D suspended by a single silk fiber. The coil is suspended between the pole-pieces N and S of permanent magnet. C is the usual iron core. The upper end of the fiber is attached to a flat spiral spring E. Spring E saves the fiber from mechanical shocks. Frame F, F carries a pointer which moves on a graduated scale. The current enters and leaves the coil by two fine silver spirals S₁ and S₂ which are connected to the terminals T₁ and T₂. A search coil of known cross-sectional area and number of turns is connected to the terminals T₁ and T₂.

Working. The search coil is placed in the space where the magnetic flux is to be measured and then withdrawn. The deflection produced in the fluxmeter is noted. The magnetic flux is directly proportional to the deflection obtained.

Theory. The flux meter coil rotates due to the induced current flowing in it when the search coil is withdrawn from magnetic flux Φ to be measured. As the coil rotates, the magnetic flux through it due the permanent magnet NS changes. Hence an induced e.m.f. is set up in the coil in a direction opposite to that due to search coil. Let e be the resultant e.m.f in the circuit. Then,

    e = e.m.f. induced due to change of magnetic flux in the search coil – e.m.f. induced in the fluxmeter coil due to its rotations in the field of permanent magnet
    = dΦ/dt – NBA dθ/dt                                … (1)

Here    N = No. of turns in fluxmeter coil.
    A = area of cross-section of fluxmeter coil.
    dθ/dt = ω = angular velocity of flux meter coil.
    B = magnetic field induction due to permanent magnet NS.
    Φ = flux from which search coil is withdrawn. It is to b e measured of fluxmeter.

Current in the circuit due to this e.m.f. is
    I = e/R’ where R is the resistance of the circuit.
Deflecting torque due to this current = NiBA
If I be the moment of inertia of the coil and ω its angular velocity at that instant, then the deflecting torque most be equal to I dω/dt. Therefore,
        NiBA = Idω/dt
or        NeBA/R = Idω/dt
or    NBA/R (dΦ/dt – NBA dθ/dt) = Idω/dt

Integrating it for time, t, for which flux changes, we have
    ∫NBA/R (dΦ/dt – NBAdθ/dt)dt = ∫ Idω/dt dt = I[ω]’0
But the coil is at rest before and after the change in flux so that ω = 0 both at t = 0 and t = t. It means right hand side is zero. Thus
    ∫¹₀ (dΦ/dt – NBA dΦ/dt) dt = 0
    ∫¹₀ dΦ/dt = NBA ∫¹₀ dθ/dt dt
or    Φ = NBAθ = kθ where k is a constant.

Hence the total change in magnetic flux linked with the search coil is directly proportional to the deflection of the moving – coil and independent of time during which the change in flux takes place.
With a lamp and scale arrangement, even a very small magnetic flux can be measure. The scale can be initially calibrated with a known flux.