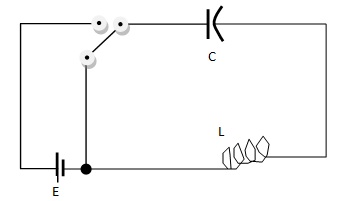
Ideal L.C. Circuit – Discharge of a Capacitor Through Inductance

Let a capacitor C, carrying a charge q0 be discharged through a coil of inductance L and negligible resistance.
Let, at any instant t during discharge, q be the charge on the capacitor and I the current in the circuit. The pd cross the capacitor is q/C and the induced emf set up in the inductances is L (di/dt). Hence the total effective emf in the circuit
        q/C – L di/dt = 0.                                    … (1)

But i = dq/dt (minus sign enters as q is decreasing with time).
. :    q/C + Ld²q/dt₂ = 0        or    d²q/dt₂ + q/LC = 0
 Or    d²q/dt² + ω²q = 0,                (where ω² = 1/LC    )                … (2)

This is a linear differential equation of second order.
The most general solution of Eq. (2) is
    Q = A1^ejωt + A2^e-jωt,                                    … (3)
Where A1 and A2 are arbitrary constants.
At t = 0, q = q₀, so that Eq. (3) gives
        q₀ = A1 + A2                                    … (4)
Differentiating Eq. (3), we get
        i = dq/dt = A₁e^jωt (jω) + A₂^e-jωt (-jω).
At t = 0, i = 0 and so we get
        0 = A1jω – A2jω
Therefore Eq. (4) gives
        A₁ = A2 =q₀/2.
Substituting in Eq. (3), we get
        q = q₀/2(ejωt  + e-jωt)
or        q = q0 cos ωt = q0 sin (ωt + π/2),                            … (5)

This is the equation of the discharge of the capacitor through the Inductance. It shows that the discharge of the capacitor is oscillatory and simple harmonic.

The period of oscillation is give by
T = 2π/ω = 2π√(LC)
The frequency of oscillation is
    f = 1/T = 1/2π√(1/LC)                                    … (6)


For more help in Ideal L.C. Circuit – Discharge of a Capacitor Through Inductance please click the button below to submit your homework assignment.