Magnetic Scalar Potential

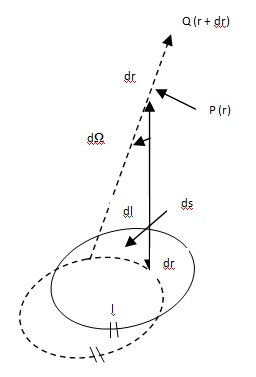
Consider a closed current loop carrying current l. Consider a point P (r) having position vector r relative to current element I dI. From Biot Savart law, the magnetic induction B at P due to whole loop is
            B = μ₀ /4π Φ I dI x r/ r₃

Let the point of observation P9r) be moved through an infinitesimal distance dr say fro P(r) to Q (r + dr). Then,
            B.dr = μ₀ /4π Φ I dI x r/r³. dr
                = μ₀ /4π Φ dr. (dI x r)/r³
                = μ₀ /4π Φ (dr x dI). r/r³

When the point P is shifted to Q, the solid angle subtended by the loop at P changes by dΩ. But we can also get the same change is solid angle dΩ by keeping P fixed and giving every point of the loop the same but opposite displacement (-dr). Then, the above equation becomes
        B.dr = - μ₀I /4π Φ (-dr x dL). r /r³

But – dr x dL = dS = area traced out by current element dI during the displacement (-dr)
    . :    B.dr = - μ₀I/4π Φ dS.r/r³

But Φ dS/r/r3 = dΩ = change in solid angle subtended by current loop when point P is displace to Q.
    . :    B.dr = - μ₀I/4π dΩ                                … (1)

Since Ω is a scalar function of (x. y. z),
        dΩ = ∇ Ω.dr
Hence Eq. (1) becomes,
B.dr = -μ₀I/4π ∇Ω.dr
Or    B = - μ₀I/4π∇Ω = - ∇ (μ₀IΩ/4π)                                … (2)

The direction of B is that of -∇Ω, so that B points away from the loop along its positive normal.

Comparing Eq. (2) with        B = -∇Vm, we get
Magnetic Scalar potential,     Vm = μ₀IΩ/4π
                    = μ₀ /4π x current x solid angle                … (3)

Negative gradient of Vm gives the magnetic induction B.