Maxwell Loop Current Method

This method employs a system a loop or mesh currents instead of branch currents. Here, the currents in different meshes are assigned continuous paths so that they do not split at a junction into branch currents. If a network has a large number of voltage sources, it is useful to use mesh analysis. This method consists of writing loop voltage equations by Kirchhoff’s voltage law in terms of unknown loop currents.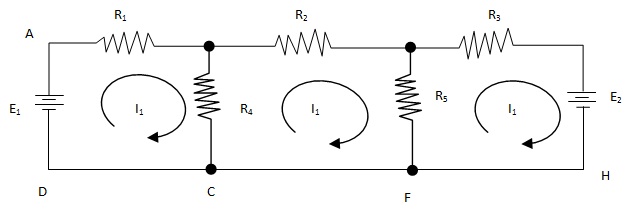



The network has two batteries (voltage sources) and five resistors. There are three meshes traversed by mesh currents I₁, I₂, I₃ respectively. Current through R₄ (when considered as a part of the first loop) is (I₁ – I₂) and that through R₅ is (I₂ – I₃). Similarly, when R₅ is considered part of the third loop, current through it is (I₃ – I₂). By applying KV to the three loops, the equations may be written as follows:

Loop 1.        E₁ – I₁R – R₄ (I₁ – I₂) = 0
Or        I₁ (R₁ + R₄) – I₂R₄ – E₁ = 0

Loop 2.        - I₂R₂ – R₅ (I₂ – I₃) – R₄ (I₂ – I₁) = 0
Or        I₁R₄ – I₂ (R₂ + R₄ + R₅) + I₃R₅ = 0

Loop 3.        - I₃R₃ – E₂ – R₅ (I₃ – I₂) = 0
Or        I₂R₅ – I₃ (R₃ + R₅) – E₂ = 0

The above three equations can be solved not only to find loop currents but branch currents as well.


For more help in Maxwell Loop Current Method click the button below to submit your homework assignment