Potential and Resistance

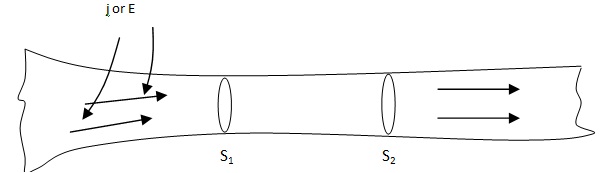
Consider the flow of current through a conductor. The current density j and the electric field E are in the same direction. The magnitude of the current between two surfaces S1 and S2 depends on the nature of the conductor and on the force which urges the free charges through it. The effect of all such forces is calculated in terms of the work performed per unit positive charge. This quantity is called the potential difference. The charge flows through the conductor in the direction of decreasing potential. Hence the potential drop
        V = V₁ – V₂ = - ∫²₁ E.dl = ∫²₁ E.dI = ∫²₁ E dI

But        E = ρj                                        … (1)
ρ is called the resistivity of the conductor.
. :    V = ∫²₁ ρ j dl

Here, the path of integration is along any line of flow from S1 to S2. If these points are brought together, the above relation reduces to zero. It is therefore clear that no static distribution of charge can produce a potential difference around a circuit. If we increase the field and potential everywhere in the same ratio, the flow lines will not change their pattern, but j will increase everywhere in the same proportion as will i. Thus we can write above relation as
        V = i∫²₁ ρ (j/i) dl.                                    … (2)
Or        V = Ri,                                         … (3)

Here, R is a quality which remains constant as V and I change but depend on the location of S1 and S2, on the flow pattern between these surfaces and on the value of ρ. This constant R is called resistance of the piece of the conductor between surfaces S1 and S2.

If the conductor is a straight and long wire of length l and area of cross section A, the lines of current flow and of electric field will be parallel. Thus E will be constant along any one line and hence, throughout the wire, So j is uniform in magnitude and direction and we can write j = i/A. Thus we have
        V = ∫²₁ ρ(i/A) dl = ρ(i/A) ∫²₁ dl = ρil/A.                        … (4)

Comparing Eqs. (3) and (4), we get
        R = ρl/A.                                    … (5)
The resistivity of the material of a conductor thus can be defined as the resistance offered by a specimen of the material of unit length and of unit area of cross section.

V, i and R are macroscopic quantities. The corresponding microscopic quantities are E, j and ρ
The resistance of a conductor between two equipotential surfaces S₁ and S₂ can be expressed in microscopic terms as
            R = V/I = ∫E. dI/∫j.dS = E∫dl/ j∫ds = El/jA = ρl/a                … (6)

We have,     div j = div(σE) = σ dive = 0.
But            E = - grad V
. :        ∇² ∇ = 0.

Thus we see that Laplace’s equation holds, as in electrostatics. In the medium, the lines of current flow are orthogonal to the lines of constant V and coincide with lines of E.




For more help in Potential and Resistance click the button below to submit your homework assignment.