Reflection and Transmission at Normal Incidence

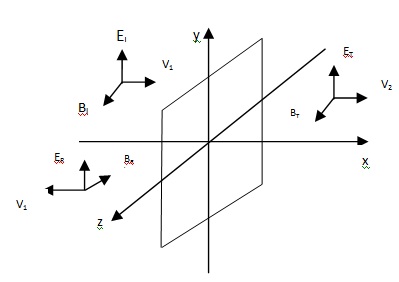
When a traveling wave reaches an interface between two difference regions, it is partly reflected and partly transmitted. Let the yz plane from the boundary between two linear media. A plane wave of frequency ω, traveling in the x direction and polarized in the y direction, approaches the interface from the left.
We can write the electric field and magnetic field of this wave as
        EI (x,t) = E₀I ei(K1x – ωt) j
        BI (x,t) = 1/v1 E₀I ei(K1x – ωt)k                            … (1)

The incident wave give rise to reflected wave in medium 1 and a transmitted wave in medium 2. The field v ectors for reflected and transmitted waves may be expressed as
        ER (x, t) = E₀R ei(-k1x-ωt)j
        BR (x, t) = -1/v1 E₀R ei(-k1x-ωt)k                            … (2)

        Er (x, t) = E₀r ei(kix-ωt)j
        Br (x, t) = 1/v2 E₀r ei(k2x-ωt)k                            … (3)

The boundary conditions at x = 0 are
(i)    ϵ1 E1 = ϵ₂ E₂|         (iii) E_1|| = E_2||
(ii)    B1| = B2|         (iv) 1/μ1 B_1|| = 1/μ2 B_2||

In this case there are no components perpendiculars to the surface. So (i) and (ii) are trivial.
From (iii)    E₀1 + E₀R = E₀r                                    … (4)

From (iv)    1/μ1 (1/v1 E₀t – 1/v1 E₀R) = 1/μ2 (1/v2 E₀r)

Or        E₀I – E₀R = βE₀r                                … (5)

Here,        β = μ1v1/μ2v2

Eqs.(4) and (5) can be solved simultaneously for the outgoing amplitudes, in terms of the incident amplitude:
        E₀R = (1-β/1+β) E₀1, E₀r = (2/1+β) E₀I                        … (7)

If the permittivities μ are close to their values in vacuum, β = v1 /v2. Then, we have
        E₀R = (v2 - v1/v2 + v1)E₀!,    e₀r = (2v2/v2 + v1) E₀I                … (8)

The reflected wave is in phase (right side up) if v2 > v1 and out of phase (upside down) if v2 < v1.
The real amplitudes are related by
        E₀R = |v2 – v1/v2 + v1|E₀1,     E₀r = (2v2/v2 + v1)E₀1                … (9)

In terms of the index of refraction,
        E₀R = |n1 – n2/n1 + n2|E₀1,     E₀r = (2n1/n1 + n2)E₀1,                … (10)

The ration of the reflected and transmitted wave amplitudes to the incident amplitude entirely by the indices of refraction of the two media.


Energy Relations. Now let us see how the incoming energy flow is divided between the reflected and transmitted waves.
The intensity of the electromagnetic wave is
        I = 1/2 ϵ vE²₀
Let μ₁ = μ₂ = μ₀. Then,
the ratio of the reflected intensity to the incident intensity is
        R = IR/II = (E₀R/E₀1) = (n₁ – n₂/n₁ + n₂)₂                        … (11)
The ratio of the transmitted intensity to the incident intensity is
        T = IT/II = ϵ₂ v₂/ ϵ₁ v₁ (E₀r/E₀¹)² = n₂/n₁(2n₁/n₁ + n₂)                 … (12)

R is called the reflection coefficient and T the transmission coefficient at the surface. They measure the fraction of the incident energy that is reflected and transmitted, respectively
Now,         R + T = 1
This result expresses the fact of energy conservation since it says that all of the incident energy appears either in the reflected wave or in the transmitted wave so that none is lost during the process.