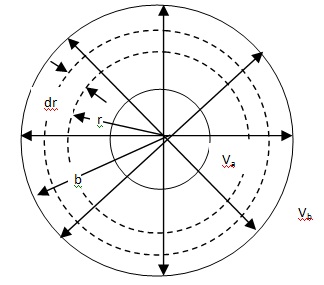
Resistance for Radial Current Through a Circular Disc

Consider the radial flow of current through a circular slab of conducting material from some radius a at a potential Va to the outer radius b at a potential Vb. Let the conductivity of the circular slab be σ and its thickness be t. The cross section of this conductor perpendicular to the current flow is 2πrt at any radius r. The cross section varies as we move out from one end of the conductor to the other. Therefore, we do not expect the voltage gradient or electric field to be uniform. However, the total current through any cross section is the same as that through any other cross section.

So we can write an expression for the current,
    i = jA = σ AE = -σ2πrt dV/dr                                … (1)
Here, j is the current density at any radius r.
The potential drop dV across a ring of width dr is
    dV= - i/2π/σ dr/r
The total voltage difference between the two ends of the conductors is
    ∫dV = - i/2πtσ ∫ba dr/r
or Va - Vb = i/2πtσ in b/a.
. : Resistance R = Va - Vb /I = 1/2π/b In b/a.

We have chosen a case in which it is easy to find the element of area that is perpendicular to the current flow. This is necessary in order to obtain i from jA as we did in Eq. (1). If the current is not perpendicular to the cross section chosen, we must use i = j. A, which complicates the problem.


For more help in Resistance for Radial Current Through a Circular Disc click the button below to submit your homework assignment.