Conservative Nature of The Electrostatic Field

Consider the field due to a point charge q. Let E be the electric field at any point P due to the point charge q.
Force on the test charge q0 = q0 E.
Hence an external force F = -q0 E is required to displace the test charge q0.

External work necessary to move the test charge through a distance dI making an angle θ with the force F is dW = F.dI.



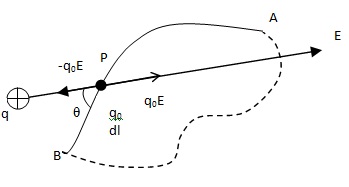
Total external work done to move the test charge q0 from A to B is
        W = ∫ F.dI = - q0 ∫ E.dI                                … (1)
E.dI = E dI cos (180 – θ) = - EdI cos θ = E dr = 1/4πε0 q/r2 dr

Let rA and rB be the radial distances of points A and B respectively from recharge q. Then,
    W = ∫ F. dI = - q0 ∫ 1/4πε0 q/r2 dr = q0 q/4πε0 [1/rB – 1/rA]                    … (2)

The work done depends only on the straight point rA and the end point rB but not on the path chosen to go from A and B.
The work done along a closed path (A to B along the continuous line + B to A along the dotted line) is thus zero.
Therefore, the field of a point charge is conservative.

Work done is a scalar quantity. So total work done is moving a charge q0 from point A to point B in an electric field due to a distribution of charges just the sum of the work required to move this test charge when charges are considered individually. Thus the field due to arbitrary distribution of charges is also a conservative field.

Line integral is independent of path. So an equivalent statement of the conservative nature of an electrostatic field is
                Φ E.dI = 0,                            … (3)
i.e., the line integral around a closed path is zero,
    or            ∫A E.dI = - ∫B E.dI                            … (4)



For more help in Conservative Nature of The Electrostatic Field click the button below to submit your homework assignment.