The field of a Small Current Loop  - The Magnetic Dipole

Consider a rectangular loop and choose out coordinates. A steady current l flows around the loop. Let A be the magnetic vector potential at P. There are no currents in the z-direction. So Az = 0. There are current in the x-direction on the two-sides of length a. In each leg, the current density is uniform. So the solution for A, is just like the electrostatic potential from two charge rods. The rods have opposite charges. Let p be the dipole moment of the charge distribution.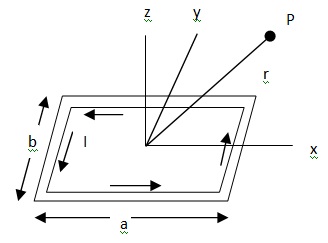

       
The potential at P is
        V = 1/4πε₀ p.r/r₂ = 1/4πε₀  p cos θ/r₂

Here, r is the unit vector along r. θ is the angle between p and r.
The direction of p is same as E with negative y-direction.
Let λ be the linear density of charge on the rods.

   
The dipole moment = total charge on one rod x separation between them.
        p = λ.a.b
Let        α = area of cross-section of the wire,
        ρ = charge per unit volume.
Then,         λ = volume of unit length of wire x ρ = αρ
Hence,         p = αρ.ab
and         1/4πε₀ p.r/r²

Now,        cos (180 – θ) = y/r or    cos θ = -y/r.
. :        V = - 1/4πε₀ αρ.ab/r²  y/r
From this, Ax is directly written by replacement of ρ/ε⁰ by μ₀ J i.e.,
        Ax = - 1/4π μ₀ J α ab/r² y/r
But        J.α = current I
. :        A_x = - μ₀ Iab/4π y/r³

Similarly, A_y can be calculated from the electric potential due to two oppositely charged rods lying parallel to y-axis separated by distance a.
        V = 1/4πε₀ p.r/r² = 1/4πε₀ αρ.ab/r²  x/r            (. : cos θ = x/r)
. :        Ay = μ₀ Iab/4π x/r³
        Az = 0

The magnitude A of the vector potential at P is
        A = (A_x² + A_y² + A_z²)^1/2
        A = μ₀I ab/4π (x₂ + y₂)^1/2 /r³
        Now, r² = x² + y² +z²             or x² + y² = r² –z².
Or        (x² + y²)^1/2 = r√1 - z²/r²
But        z/r = cos θ_z

. :        A = μ₀ I ab/4π 1/r² √1- cos² θ_z

Here, θ_z is the angle which r makes with z-axis.
        A = μ₀ /4π I ab sin θ_z /r²

We call the produce current x area (Iab) the magnetic dipole moment of the current loop and denote it by m. Hence,
    A = μ₀ /4π m sinθ_z /r² = μ₀ /4π m x r/r²                         … (4)

This will be the same at every point on a circle around the dipole. A is perpendicular to the plane containing the dipole and point of observation.
Now the magnetic induction B can be determined by taking the curl of Eq. (4)

    B(r) = curl A (r) = curl {μ₀ /4π m x r/r²}
    B_x = (∂A_z /∂_y) – (∂A_y /∂_z) = - ∂A_y /∂_z, since A_z = 0

Substituting Ay from Eq. (2),
    B_x = - ∂/∂_z (μ₀m/4π. x/r₃) where m = Iab and r = (x² + y² + z²)^1/2
. :     B_x = μ₀m/4π . 3xz/r⁵
Similarly,    By = μ₀m/4π. 3yz/r⁵
        B_z = ∂A_y/∂_x - ∂A_x/∂_y

Substituting the values from Eqs. (1) and (2),
        B_z = μ₀m/4π [∂(x/r³)/∂x + ∂(y/r³)∂y)]
         = μ₀m/4π [2/r³ – 3/r⁵ (x² + y²)]
        B_z = - μ₀m/4π (1/r³ – 3z² /r⁵)

The magnitude B of the magnetic induction at P is
        B = [B_x² + B_y² + B_z²]^1/2
. :        B = μ₀m/4π³ √1 + 3cos²θ                                … (5)

This expression is same as that of the electric dipole oriented along the z-axis. The current loop is, therefore, called a magnetic dipole.


For more help in The field of a Small Current Loop  - The Magnetic Dipole click the button below to submit your homework assignment