The Magnetic Dipoles

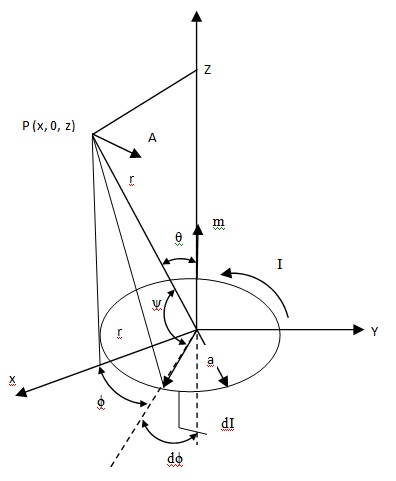
Consider a circular loop of wire of radius a, situated at the origin in a plane perpendicular to the z-axis and carrying a current I. We shall first calculate the vector potential A at a point P on the x-axis z-plane.
The vector potential dA at this point due to an element dI is
        dA = μ₀ /4ππ I dI/r’
Since dI is in x-plane, dA is in x-y plane.

For any given value of r’, we can consider two symmetrical dI elements whose y-components add and whose x-components cancel. Then we need only calculated the y, or azimuthally components of A. Thus total vector potential due to the whole loop is
            A = μ₀/4π I ʃ dI/r’ cos Φ
            = μ₀/4π I ʃ (adΦ) cos ɸ/r’ Φ1.

Here, Φ₁ is the azimuthally unit vector in spherical polar coordinates.
 0.
We must now express r’ in terms of r and of ψ.
        r’² = r² + a² – 2ar cos ψ.
Or        1/r’ = 1/r [1 + a²/r2 – (2a/r) cos ψ]1/2 = 1/r [1 – a² /2r² + a/r cosψ]

We have assumed here that a << r. To replace cos ψ, let us write r.a in two ways and compare (xi + zk).(a cos Φi + a sin Φj) = ra cos ψ or x cos Φ = r cos ψ.
. :     1/r’ = 1/r [1 – a² /2r² + ax/r² cos Φ   

and     A = μ₀I/4π ʃ a cos ɸ/r [1 – a² 2r² + ax cos ɸ/r² ]dɸ
    = μ₀ /4π Iπa² r³ x = μ₀ 4π Iπa² r² sinθ = μ₀ 4π / mr² sin θ.
Or     A = μ₀ /4π m x r¹ /r² = μ₀ /4π ∇ x m/r,

Here m is the dipole moment, given by m = I(πa²)k =  IS.
r¹ is a unit vector.

To find B, we simply compute ∇ x A.
The magnetic induction B is given by
        B = ∇ x A μ₀ /4π ∇ [m.∇(1/r)].
Here we have used relations ∇x ∇ x A = ∇ (∇.A) - ∇2 A and ∇2 (1/r) = 0- for r ≠ 0.

The relation for B is of the same form as the expression for the electgric field due to an electric dipole of dipole moment P:
        E = 1/4πε₀ ∇ [p. ∇ (1/r)].

Thus the electric and magnetic dipoles give rise to similar field.