Theory of the Transformer

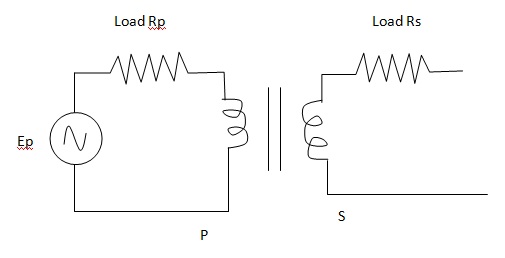
1.    Transformer on no load

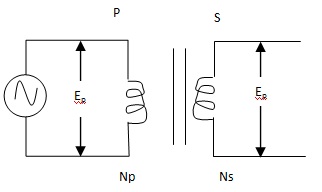
Let NP and NS be the number of turns in the primary and secondary respectively of the transformer. When an alternating emf is applied across the primary, a current flows in its winding. The develops a magnetic flux in the core. Here it is assumed that there are no losses and no leakage of flux. Let Φ = flux linked with each turn of either coil. This magnetic flux is linked up with both the primary and the secondary.

By Faraday’s law of electromagnetic induction, the emf induced in the primary is given by
            ε_p = - d (N_p Φ) /dt = - N_p dΦ/dt

and the emf induced in the secondary,
            ε_s = - d (N_s Φ)/dt = - N_s dΦ/dt

. :            ε_s / ε_p = N_s /N_p .

In an ideal transformer, the resistance of the primary of the primary circuit is negligible and there are no energy losses. So the induced emf εp in the primary is numerically equal to the applied voltage Ep across the primary. If the secondary is an open circuit, its resistance is infinite. So the voltage Es across the terminals of the secondary is equal to the induced emf εs.

            E_s/E_p = ε_s/ε_p = N_s/N_p = K,                … (1)

Where K is called the turns ratio or transformation ratio of the transformer.
K =    Voltage obtained across secondary         =     No. of turns in secondary
     ___Voltage applied across primary         _____   No. of turns in primary

In a step-up transformer εs > εp and hence N_s > N_p.
In a step-down transformer εs < εp and hence N_s < N_p.

Let Ip and Is be the currents in primary and secondary at any instant.
In this case power output is equal to power input.
Power in the secondary = power in the primary
    E_s X I_s = E_p x I_p
    I_p / I_s = E_s / E_p = N_s/N_p = K.                            … (2)

Thus, when the voltage is stepped-up, the current is correspondingly reduced in the same ratio, and vice-versa.

(ii) Transformer on load

If the primary circuit has an appreciable resistance R_p, the difference between the applied voltage E_p and the back e.m.f. εp must be equal to the potential drop I_p x R_p in the primary coil, i.e.,
        E_p – ε_p = I_p x R_p.
or                 Ε_p = E_p – I_p x R_p                         … (3)

Again, if the secondary circuit is closed having finite resistance Rs, a part of the induced emf εs in the secondary overcomes the potential drop is x Rs. Hence the available P.D. across the secondary is given by
        E_s = ε_s - I_s x R_s
Or        ε_s = E_s + I_s x R_s
    Hence    ε_s/ε_p = E_s + I_sR_s /E_p - I_pR_p = K
Or     E_s + I_sR_s = K (E_p – I_p-R_p)
    E_s     = KE_p – I_sR_s – KI_pR_p
        = KE_p – I_sR_s – K²I_sR_p                        ( . : I_p = K I_s)
        = KE_p – I_s (R_s + K²R_p)
In this case E_s/E_p is not a constant but decreases as more current is drawn from the secondary circuit.