Maxwell Circulating Current Theorem
Maxwell Circulating Current Theorem Assignment Help | Maxwell Circulating Current Theorem Homework Help
Maxwell Circulating Current Theorem
This theorem is applied for solution of networks having more than two terminals. For applying this method of solution to a complicated network is divided into meshes or closed circuits and in each mesh a separate current is assumed to circulate. By this theorem the current flowing through the section common to two meshes will be equal to the algebraic sum of the currents in the later two meshes. The direction of any mesh current may be taken either as clockwise or as counter-clockwise but for systematic solution the directions of all mesh currents are assumed to the same (say clock-wise). Then Kirchhoff’s second law is applied to each mesh and algebraic equations are obtained. By soling these equations unknown quantities can be determined. This method eliminates a great deal of tedious calculation work involved in the branch current method, adopted so far.
Application of Maxwell circulating current theorem will be more clear from the following illustrations,
Q. Solve the network shown below to find the current in 2, 3 and 4-Ω resistors.
Solutions: The network is shown in. There are flowing lasing the loops have been taken as clockwise. The individual branch currents along with their direction of flow are also shown in the circuit diagram. Applying Kirchhoff’s second law to these two meshes I and II we get
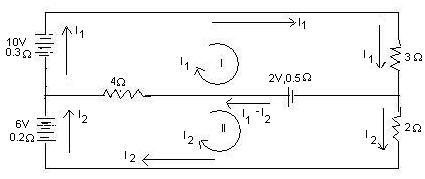
3 I1 + 0.5 (I1-I2) + 4 (I1-I2) + 0.3 I1 = 10+2
or 7.8 I1-4.5 I2 = I2
and 2 I2 + 0.2 I2-4 (I1-I2)- 0.5 (I1-I2) = 6-2
or 6.7 I2-4.5 I1 = 4
Multiplying expression (i) by 1.5 and expression (ii) by 2.6 we get
11.7 I1-6.75 I2 = 18
17.42 I2-11.7 I1 = 10.4
Adding expressions (iii) and (iv) we get
10.67 I2= 28.4
I2 = 28.4 = 2.66 A
10.67
Substituting I2 = 2.66 in expression (i) we get
7.8 I1-4.5 X 2.66 = 12
I2 = 12+ 11.97 = 3.073 A
7.8
Now current through 2- Ω resistor = I2 = 2.66 A
current through 3- Ω resistor = I1 = 3.073 A
current through 4- Ω resistor = I1-I2 = 3.073-2.66 = 0.413 A
For more help in Maxwell Circulating Current Theorem click the button below to submit your homework assignment
Application of Maxwell circulating current theorem will be more clear from the following illustrations,
Q. Solve the network shown below to find the current in 2, 3 and 4-Ω resistors.
Solutions: The network is shown in. There are flowing lasing the loops have been taken as clockwise. The individual branch currents along with their direction of flow are also shown in the circuit diagram. Applying Kirchhoff’s second law to these two meshes I and II we get
3 I1 + 0.5 (I1-I2) + 4 (I1-I2) + 0.3 I1 = 10+2
or 7.8 I1-4.5 I2 = I2
and 2 I2 + 0.2 I2-4 (I1-I2)- 0.5 (I1-I2) = 6-2
or 6.7 I2-4.5 I1 = 4
Multiplying expression (i) by 1.5 and expression (ii) by 2.6 we get
11.7 I1-6.75 I2 = 18
17.42 I2-11.7 I1 = 10.4
Adding expressions (iii) and (iv) we get
10.67 I2= 28.4
I2 = 28.4 = 2.66 A
10.67
Substituting I2 = 2.66 in expression (i) we get
7.8 I1-4.5 X 2.66 = 12
I2 = 12+ 11.97 = 3.073 A
7.8
Now current through 2- Ω resistor = I2 = 2.66 A
current through 3- Ω resistor = I1 = 3.073 A
current through 4- Ω resistor = I1-I2 = 3.073-2.66 = 0.413 A
For more help in Maxwell Circulating Current Theorem click the button below to submit your homework assignment