Consider a fluid element ABCD rotating at a uniform velocity in a horizontal plane about an axis O.


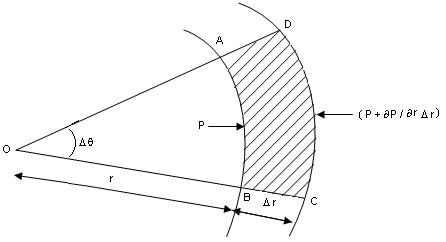
Let  r = radius of element from O
       Δ r = radial thickness of the element
      ΔA = Area of cross-section f element
      Δθ = Angle subtended by the element at O.

The force acting on the element are

(i)    Centrifugal force. mv² / r acting away from the centre at O,
(ii)    Pressure force P. ΔA on the face AB
(iii)    Pressure force ( P + ∂P / ∂r Δr ) ΔA on the face CD.

Equating the forces in radial direction,

Net force  =  Time rate change of momentum

( P + ∂P / ∂r Δr ) ΔA-P.   ΔA = mv² / r

but mass  =  mass density x volume

m  = ρ. ΔA. Δr

∂P / ∂r Δr.  ΔA = ρ. ΔA. Δr v² / r

∂P / ∂r = ρ. v² / r

The expression ∂P / ∂r is called pressure gradient in the radial direction

As ∂P / ∂r is positive, hence pressure increases with the increase of radius r.

The pressure variation in the vertical plane is given by hydrostatic law,

∂P / ∂z = -Pg

As the pressure is the function of r and z, therefore total derivative of P.

dp = ∂P / ∂r dr +∂P / ∂z  dz

Substituting the values of ∂P / ∂r and ∂P / ∂z from equation

dp = ρv² / r dr- ρ g dz

Equation gives the variation of pressure of a rotating fluid in any plane.

For more help in Equation of Motion For Vortex Flow click the button below to submit your homework assignment