Rotation
Rotation Assignment Help | Rotation Homework Help
Rotation
Rotation is defined the movement of a fluid element in such a way that both of its horizontal as well as vertical axes rotate in the same direction.
Rotational flow:
Flow is said to be rotation, when every fluid element rotates at its axis which is perpendicular to the plane of motion.
Consider a rectangular fluid element ABCD at a certain time in a two-dimensional x-y plane.
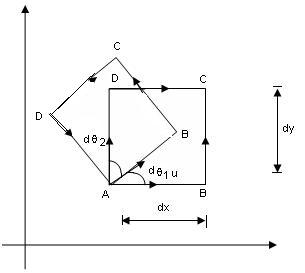
The velocity components x-direction at A and D are,
u and [ u + ∂u / ∂y . dy ] respectively.
The velocity component in y-direction at B and D are.
v and [ v + ∂v / ∂x . dx ] respectively.
Since these velocities are different, there will be angular velocity developed for linear element AD and AB respectively.
In time interval ‘dt’ the elements AB and AD would move relative to point A, the fluid element takes position AB’C’D’.
Consider anti-clockwise rotation as positive, the angular velocity of element AB at
z-axis is,
We know, L = r θ and ω = dθ / dt
ωAB = Angular displacement of AB / time
= [ ( v + ∂v / ∂x . dx ) - v ] dt / dx = v dt / dx + ( ∂v / ∂x .dx ) dt / dx / dt
ωAB = ∂v / ∂x
Perpendicularly angular displacement at AD about Z-axis,
ωAD = ∂u / ∂y
The average of angular velocities of two mutually perpendicular elements gives the rotation about Z-axis.
ωAD = 1/2 [ ∂u / ∂X - ∂u / ∂y ]
For these dimensional fluid, there-rotational components is given by,
ωx = 1/2 [ ∂w / ∂y - ∂v / ∂z ]
ωy = 1/2 [ ∂u / ∂z - ∂w / ∂x ]
ωz = 1/2 [ ωx / ∂x - ∂u / ∂y ]
Rotational vector, ωx = ωx i + ωy j + ωz k = 1/2 Curl v
Condition for rotational flow,
ωx = 0 ωy = 0 ωz = 0
Substituting u = - ∂Φ / ∂x and v = ∂Φ / ∂y in equations
Rotational components,
ωz = 1/2 [ ∂v / ∂x - ∂u / ∂y ] = 1/2 [ ∂ / ∂x (-∂Φ / ∂y) - ∂ / ∂y (-∂Φ / ∂x) ]
= 1/2 [ -∂2Φ / ∂x .∂y + ∂2Φ / ∂y. ∂x
Perpendicularly, ωz = 1/2 [ -∂2Φ / ∂y .∂z + ∂2Φ / ∂z. ∂y ]
ωz = 1/2 [ -∂2Φ / ∂z .∂x + ∂2Φ / ∂x. ∂z ]
If Φ is continuous function,
[ -∂2Φ / ∂y .∂z + ∂2Φ / ∂z. ∂y ] , [ -∂2Φ / ∂z .∂x + ∂2Φ / ∂x . ∂z ] , [ -∂2Φ / ∂x .∂y + ∂2Φ / ∂y. ∂x ]
For more help in Rotation click the button below to submit your homework assignment
Consider a rectangular fluid element ABCD at a certain time in a two-dimensional x-y plane.
The velocity components x-direction at A and D are,
u and [ u + ∂u / ∂y . dy ] respectively.
The velocity component in y-direction at B and D are.
v and [ v + ∂v / ∂x . dx ] respectively.
Since these velocities are different, there will be angular velocity developed for linear element AD and AB respectively.
In time interval ‘dt’ the elements AB and AD would move relative to point A, the fluid element takes position AB’C’D’.
Consider anti-clockwise rotation as positive, the angular velocity of element AB at
z-axis is,
We know, L = r θ and ω = dθ / dt
ωAB = Angular displacement of AB / time
= [ ( v + ∂v / ∂x . dx ) - v ] dt / dx = v dt / dx + ( ∂v / ∂x .dx ) dt / dx / dt
ωAB = ∂v / ∂x
Perpendicularly angular displacement at AD about Z-axis,
ωAD = ∂u / ∂y
The average of angular velocities of two mutually perpendicular elements gives the rotation about Z-axis.
ωAD = 1/2 [ ∂u / ∂X - ∂u / ∂y ]
For these dimensional fluid, there-rotational components is given by,
ωx = 1/2 [ ∂w / ∂y - ∂v / ∂z ]
ωy = 1/2 [ ∂u / ∂z - ∂w / ∂x ]
ωz = 1/2 [ ωx / ∂x - ∂u / ∂y ]
Rotational vector, ωx = ωx i + ωy j + ωz k = 1/2 Curl v
Condition for rotational flow,
ωx = 0 ωy = 0 ωz = 0
Substituting u = - ∂Φ / ∂x and v = ∂Φ / ∂y in equations
Rotational components,
ωz = 1/2 [ ∂v / ∂x - ∂u / ∂y ] = 1/2 [ ∂ / ∂x (-∂Φ / ∂y) - ∂ / ∂y (-∂Φ / ∂x) ]
= 1/2 [ -∂2Φ / ∂x .∂y + ∂2Φ / ∂y. ∂x
Perpendicularly, ωz = 1/2 [ -∂2Φ / ∂y .∂z + ∂2Φ / ∂z. ∂y ]
ωz = 1/2 [ -∂2Φ / ∂z .∂x + ∂2Φ / ∂x. ∂z ]
If Φ is continuous function,
[ -∂2Φ / ∂y .∂z + ∂2Φ / ∂z. ∂y ] , [ -∂2Φ / ∂z .∂x + ∂2Φ / ∂x . ∂z ] , [ -∂2Φ / ∂x .∂y + ∂2Φ / ∂y. ∂x ]
For more help in Rotation click the button below to submit your homework assignment