Chi Square Distribution

Population

A population consists of the totality of the observation, with which we are concerned.

Sample

A sample is a subset of a population.

Random variable

A random variable is a function that associates a real number with each element in the sample.

Probability Density Function

It is defined as the relative likelihood that value of the subject variable is equal to that if the sample

Normal Distribution

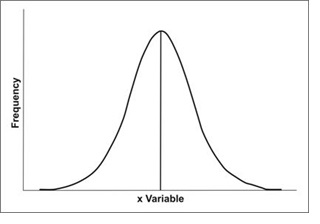
An extremely common statistical distribution. Also called natural or Gaussian distribution. Standard Normal Distribution is a special case of normal distribution with mean, μ = 0 and standard deviation,σ = 1.A random variable X having a normal distribution is said to be normally distributed.

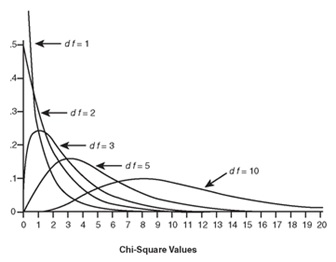
Chi-Square or Chi-Squared distribution of ‘k’ degrees of freedom is defined as the distribution of sum of ‘k’ standard normal variables. It is an extremely important statistical distribution, given its use in the field data analytics for hypothesis testing and to determine confidence intervals. Thus, let understand the concept by example.

Suppose we have anormally distributed random variable ‘X’ with mean ‘μ’ and standard deviation ‘σ’. To make this distribution standard normal we define:

Y = (X – μ) /σ

Thus, Z = Y2 is said to have a chi-square distribution of degree 1. Similarly, Z = Y12 + Y12 + … + Yn2, is said to be a Chi-Square distribution of degree ‘n’. Meaning:

Z ~ χ2n

Thus, clearly greater degree of freedom indicated greater probability of larger variable.